HTML+CSS+JS实现一个特殊的时钟
介绍：
迄今为止，中国历史上记载的钟表已经历了四代：日晷、沙漏、机械钟、石英钟，其中石英钟是中国市场上最受欢迎的钟表。
钟表一直是中国人最喜爱的商品之一。新中国成立后，国家投入大量资金发展钟表业，使这一行业得到了迅速发展。此后，中国的改革开放和经济全球化给中国钟表业带来了繁荣。经过几十年的发展，中国钟表业经历了来料组装-外观件制造-产品开发-品牌创立的发展历程，形成了完整的钟表制造业，除高端机芯外，所有零部件均可加工生产。
现状：
1.企业数量结构
我国钟表行业共有3600多家钟表企业，其中包括飞亚达、海鸥、罗西尼等知名企业。这些企业主要集中在广东，从事钟表相关产品配套的企业约有2000家。其中，2019年规模以上企业数量达到260家。
2. 员工规模
据统计，2019年全国规模以上从事钟表生产的企业从业人员总数约10万人，其中，国产知名品牌2019年从业人员数量达4994人。
3.行业资产规模
近年来，我国大型钟表制造企业资产总额都在400亿元左右，据统计，2019年，我国大型钟表制造企业资产总额达到408亿元。
四、行业市场规模
钟表行业是与人们生活息息相关的高精密制造业，2019年我国钟表行业工业企业260家，营业收入363亿元，利润22.3亿元，我国钟表产量占世界钟表产量的90%，占世界手表产量的80%，是名副其实的钟表生产大国，正在向钟表生产强国迈进。
影响：
实施代码
本文主要使用js实现功能，利用js中的，可以制作出强大的前端效果。
中文名叫“画布”，是游戏中所有UI组件的“容器”。在一个场景中，可以存在多个物体，它们之间可以“嵌套”，需要注意的是，场景中任何一个UI物体都必须是某个物体的“子级”。
索引.html
DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<link rel="stylesheet" href="style.css">
<script src="script.js" defer>script>
<title>Documenttitle>
head>
<body>
<canvas id="canvas">canvas>
<div id="clock">div>
body>
html>
.js
var canvas = document.getElementById("canvas")
canvas.width = 400
canvas.height = 400
var ctx = canvas.getContext("2d")
var clock = document.getElementById("clock")
var colors = ["#1e90ff", "#2ed573", "#ff6348"]
function draw() {
ctx.clearRect(0, 0, canvas.width, canvas.height)
var d = new Date()
var secdeg = d.getSeconds() * 6 + d.getMilliseconds() * 6 / 1000
var mindeg = d.getMinutes() * 6 + secdeg / 60
var hourdeg = d.getHours() % 12 * 30 + mindeg / 60
var lines = [hourdeg, mindeg, secdeg]
ctx.lineWidth = 10
ctx.lineCap = "round"
ctx.beginPath()
for (var i = 0; i < 3; i++) {
ctx.beginPath()
ctx.arc(200, 200, 140 + i * 20, 0, Math.PI * 2)
ctx.strokeStyle = "#222"
ctx.stroke()
ctx.beginPath()
ctx.arc(200, 200, 140 + i * 20, -Math.PI / 2, Math.PI / 180 * lines[i] - Math.PI / 2, 0)
ctx.strokeStyle = colors[i]
ctx.stroke()
}
for (var i = 0; i < 12; i++) {
var bx = 200 + 180 * Math.cos(i * 30 * Math.PI / 180)
var by = 200 + 180 * Math.sin(i * 30 * Math.PI / 180)
ctx.fillStyle = "#6FD08C"
ctx.beginPath()
ctx.arc(bx, by, 3, 0, Math.PI * 2)
ctx.fill()
}
var x = 10 * Math.cos((secdeg + 90) * Math.PI / 180)
var y = 10 * Math.sin((secdeg + 90) * Math.PI / 180)
clock.style.textShadow = x + "px " + y + "px 5px hsl(" + (mindeg | 0) + ",30%,30%)"
clock.style.color = "hsl(" + (mindeg | 0) + ",80%,50%)"
clock.innerText = ("0" + d.getHours()).slice(-2) + ":" + ("0" + d.getMinutes()).slice(-2) + ":" + ("0" + d.getSeconds()).slice(-2)
requestAnimationFrame(draw)
}
draw()
样式.css
* {
margin: 0;
padding: 0;
}
body {
background: #333;
width: 100%;
height: 100vh;
display: flex;
justify-content: center;
align-items: center;
}
#clock {
position: absolute;
/* color: white; */
font-size: 50px;
font-weight: bold;
font-family: Arial, Helvetica, sans-serif;
}
每天一道算法题，动态求连续区间之和
给定一个由 n 个数字组成的序列，指定两个操作：一是修改某个元素，二是求子序列 [a, b] 的连续和。
输入格式
第一行两个整数n和m，分别表示数字个数和操作次数。
第二行包含n个整数，表示完整的序列。
接下来的 m 行每行包含三个整数 k, a, b （k=0，表示求子序列 [a, b] 的和；k=1，表示将第 a 个数字加到 b 上）。
序列从 1 开始计数。
输出格式
输出几行数字，表示k=0时相应子序列[a,b]的连续和。
数据范围
1≤n≤，
1≤m≤，
1≤a≤b≤n，
数据保证在任何时候，序列中所有元素的总和都在 int 范围内。
示例输入：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
示例输出：
11
三十
三十五
算法思路
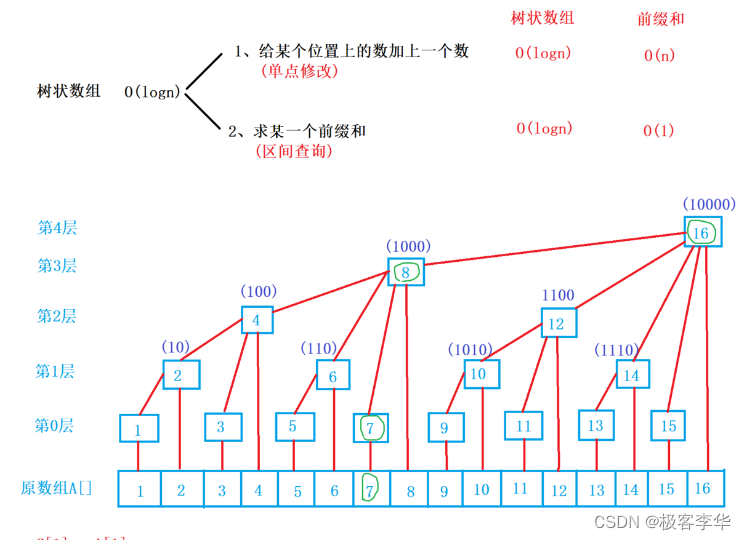
1. (x)：返回 x 的最后一位数字（1）
2. add(x,v)：将 v 添加到 x 位置，并将 v 添加到后续关联位置
3. query(x): 查询前缀和
具体代码
C++
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int w[N];
struct Node{ // 这个Node的含义为区间[l, r]的sum值是多少 线段树的本质就是一个二叉树 所以后面的所有操作本质就是二叉树的那一套
int l, r;
int sum;
}tr[4 * N];
void push_up(int u) // 通过左右孩子计算父亲的值的函数
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; // 父节点的值 等于左右孩子的值相加 u << 1 相当于 u * 2；
}
void build(int u, int l, int r) // 建立线段树的函数 第一个参数为当前结点的编号，第二个参数为左边界，第三个参数为右边界
{
if (l == r) tr[u] = {l, r, w[r]}; // 如果当前结点已经是叶子节点了 那么就可以直接把权值赋值给这个 线段树上面的结点了
else // 如果当前区间的左右边界不相同 说明当前区间的长度至少是2（这里的理解可以通过看线段树的图来理解，线段树是一个大区间不断分成一个一个的小区间）
// 直到分到不能再分为止 如果这个区间的长度不小于2 那么这个区间的左右边界 就不相等 那么这个区间就可以继续分
{
tr[u] = {l, r}; // 先对u这个结点的左右边界赋值一下 规定这个u结点表示的区间范围
int mid = l + r >> 1;
// 把结点u的左右儿子都算出来
build(u << 1, l, mid); // 先递归下左儿子
build(u << 1|1, mid + 1, r); // 再递归下右儿子
push_up(u); // 然后再通过这个函数算出u结点 包含区间的值
}
}
int query(int u, int l, int r) // 查询的过程是从根结点开始往下找对应的区间的 所以第一个参数可以说默认就是1了
{
if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum; // 如果当前的这个结点所表示的区间被 我们需要的区间
// 完全包含 那么就直接返回这个区间的值
// 反之就对没有完全包含的子区间 分割 知道 分到 子区间的某个子区间 被完全包含为止
int mid = tr[u].l + tr[u].r >> 1; // 先计算下 当前这个区间 与[l, r]有没有交集 交集在那一部分
int sum = 0; // 区间[l, r]的和
// 这两句话的理解要加上二叉树的那个图像 才好理解 本质就是不断缩小区间然后 知道 寻找到一个u的左右边界 被[l, r]
// 完全包含
if (mid >= l) sum += query(u << 1, l, r); // 看看当前的区间的中点与待查区间的左边有没有交集
if (mid + 1 <= r) sum += query(u << 1 | 1, l, r); // 再看看这个u这个区间的中点与[l, r]的右边有没有交集
return sum;
}
void modify(int u, int x, int v) // 第一个参数还是默认根结点， 后面就是 在x的基础上加上v
{
if (tr[u].l == tr[u].r) tr[u].sum += v; // 找到根结点了
else
{
int mid = tr[u].l + tr[u].r >> 1;
// 寻找一下x是在u结点区间的左半边还是右半边
if (x <= mid) modify(u << 1, x, v); // 在左半边的情况
else modify(u << 1 | 1, x , v); // 在右半边的情况
// 更新完之后在往上把与被修改的叶子结点 有关联的父结点的值都修改一遍
push_up(u);
}
}
int main()
{
scanf ("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i) scanf ("%d", &w[i]);
build(1, 1, n); // 构建 [1, n]区间的线段树
while (m --)
{
int k, a, b;
scanf ("%d%d%d", &k, &a, &b);
if (!k) printf("%d\n", query(1, a, b));
else modify(1, a, b);
}
return 0;
}
Java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int N = 100010;
static int n;
static int m;
static int[] w = new int[N];
static Node[] tr = new Node[N * 4];
//用子节点信息来更新当前节点信息（把信息往上传递）
public static void pushUp(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
//在一段区间上初始化线段树，其中u表示根结点，l表示左边界，r表示右边界
public static void build(int u,int l,int r)
{
if(l == r) tr[u] = new Node(l,r,w[r]);
else
{
tr[u] = new Node(l,r,0);
int mid = l + r >> 1;
build(u << 1,l,mid);
build(u << 1 | 1,mid + 1,r);
pushUp(u);
}
}
//查询某段区间的和，其中u表示根结点，l表示左边界，r表示右边界
public static int query(int u,int l,int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
int mid = tr[u].l + tr[u].r >> 1;
int sum = 0;
if(l <= mid) sum = query(u << 1,l,r);
if(r > mid) sum += query(u << 1 | 1,l,r);
return sum;
}
//修改操作，在u结点中，x位置加上v
public static void modify(int u,int x,int v)
{
if(tr[u].l == tr[u].r) tr[u].sum += v;
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u << 1,x,v);
else modify(u << 1 | 1,x,v);
pushUp(u);
}
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String[] s1 = reader.readLine().split(" ");
n = Integer.parseInt(s1[0]);
m = Integer.parseInt(s1[1]);
String[] s2 = reader.readLine().split(" ");
for(int i = 1;i <= n;i++) w[i] = Integer.parseInt(s2[i - 1]);
//搭建线段树
build(1,1,n);
while(m -- > 0)
{
String[] s3 = reader.readLine().split(" ");
int k = Integer.parseInt(s3[0]);
int x = Integer.parseInt(s3[1]);
int y = Integer.parseInt(s3[2]);
//k = 0 是询问[x,y]的区间和，k = 1是在x位置添加y元素
if(k == 0) System.out.println(query(1,x,y));
else modify(1,x,y);
}
}
}
//段结点
class Node
{
public int l;//左边界
public int r;//右边界
public int sum;//当前块的总和
public Node(int l,int r,int sum)
{
this.l = l;
this.r = r;
this.sum = sum;
}
}
扫一扫在手机端查看
-
Tags : html css js怎么让时钟实时更新
- 上一篇：阿里云域名解析网址_腾讯云域名解析到阿里云服务器怎么用
- 下一篇：域名注册商跑路了怎么办_行业周报丨监管要求报送4类在售健康险产品清单；个人养老金保险产品增至98款；8家保险机构合计被罚1993万元；一人被终身禁业!
本文链接：https://by928.com/4545.html 转载请注明出处和本文链接！请遵守
《网站协议》
！
我们凭借多年的网站建设经验，坚持以“帮助中小企业实现网络营销化”为宗旨，累计为4000多家客户提供品质建站服务，得到了客户的一致好评。如果您有网站建设、网站改版、域名注册、主机空间、手机网站建设、网站备案等方面的需求，请立即点击咨询我们或拨打咨询热线： 13761152229，我们会详细为你一一解答你心中的疑难。
我们凭借多年的网站建设经验，坚持以“帮助中小企业实现网络营销化”为宗旨，累计为4000多家客户提供品质建站服务，得到了客户的一致好评。如果您有网站建设、网站改版、域名注册、主机空间、手机网站建设、网站备案等方面的需求，请立即点击咨询我们或拨打咨询热线： 13761152229，我们会详细为你一一解答你心中的疑难。
客服1 